『フェルマーの最終定理』とは?
“フェルマーの最終定理”とは十七世紀フランスの数学者ピエール・ド・フェルマーが考えた数学界屈指の難問です。
歴史に名を残す名だたる数学者たちが挑んだものの証明には至らず、350年以上の間未解決の問題として君臨し続けました。
数学をある程度学んだことがある方であれば、共感出来るかと思いますが、数学の難しさの半分はその問題を理解することにあります。
しかし、この“フェルマーの最終定理”においては例外です。
難しさの反面、問題の内容自体は非常に単純で以下の通りです。

もっと噛み砕くと、以下の通りです。
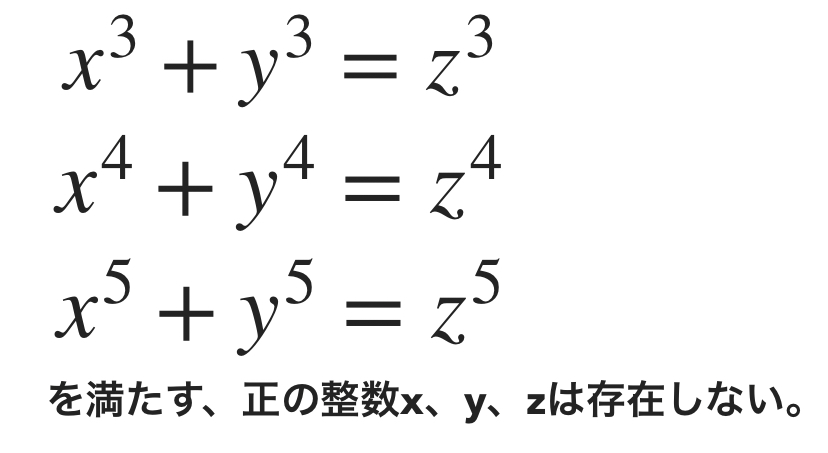
nに数字を代入したものです。これは無限に続いていきますが今回は5までしか書いていません。
たったこれだけの問題ですので理解するだけであれば、ピタゴラスの定理に馴染みがある中学生でも出来ますね。
この問題の単純さが多くの人間を数学界屈指の難問に挑ませた理由の1つでもあります。
フェルマーの最終定理は解決済みの問題である
この“フェルマーの最終定理”は1995年、天才的数学者アンドリュー・ワイルズとリチャード・テイラーらの二人によって既に解決されています。
志村・谷山・ヴェイユ予想を証明する形での解決ですが、モジュラー形式やファルティングスの定理、ケン・リベットによって証明されたフライ・セール予想など近代的アプローチの数々が可能にした高度な証明です。
しかし、そうなれば1つ疑問が残ります。
それはフェルマーがどのような解答を準備していたのか?という点についてです。
彼はディオファントスの著書『算術』の余白にこう記したと言われています。
私はこの命題の真に驚くべき証明をもっているが、余白が狭すぎるのでここに記すことはできない
サイモン・シン『フェルマーの最終定理』 訳 青木薫 新潮文庫 2006年
しかし、実際にはこの証明が後世に残されることはありませんでした。
この問題を残したフェルマーが350年以上前に、この問題を証明していたとすれば、彼は単純に考えて350年以上先の数学を見ていたことになります。
如何に天才的な数学者といえど、それは考え難いところです。
フェルマーによる証明は勘違いである可能性
現在、フェルマーの考えていた証明は、フェルマーが無限降下法による証明が可能だと勘違いしたのではないかと考えられています。
無限降下法とは背理法の一種で、自然数あるいは自然数の部分集合には必ず最小の元が存在するという性質を用いた証明方法です。
フェルマーはこの証明法を好んで使っていたと言われています。
350年以上先を見通した証明をしたのか、または誰にも及びもつかない証明をしていたのか、実際に彼の行った証明というものがどういったものであったのか、今となっては神のみぞ知るところです。
もし誰も考えつかないような証明であったのであれば、数学の世界はまた新しい世界を開くことになるでしょう。
あまり勉学を好む性格ではありませんでしたが、これには夢を感じずにはいられませんね。
最後までお読みいただきありがとうございました。

